Начертательная геометрия. Теория
Контрольные задания по теме:
Рабочая тетрадь задача 20а , задача 20б , задача 21 ,
задача 22 , задача 23
Проекцией прямой, которая не перпендикулярна плоскости проекций, является прямая. Её положение определяется двумя точками, следовательно, для того чтобы построить проекцию прямой, достаточно построить проекции двух её точек.
а) Прямой общего положения называется прямая, которая не параллельна и не перпендикулярна ни одной из плоскости проекций. Пример такой прямой изображён на рисунке 8. Комплексный чертёж этой прямой будет выглядеть следующим образом.
Рисунок 9
б) Прямые частного положения - это прямые, занимающие по отношению к плоскостям проекций особое положение, т.е. либо параллельные, либо перпендикулярные плоскостям проекций.
Первый подкласс прямых частного положения - прямые уровня. Это прямые, параллельные какой-либо плоскости проекций.
Горизонталь - прямая параллельная горизонтальной плоскости П1. Комплексный чертёж такой прямой изображён на рисунке 10.
Рисунок 10
Фронтальная проекция горизонтали всегда параллельна прямой Х, а угол между осью Х и горизонтальной проекцией горизонтали составляет угол между прямой и фронтальной плоскостью проекций. Символическая запись: h // П1; α = Ð h П2.
Фронталь - прямая параллельная фронтальной плоскости П2. Комплексный чертёж фронтали изображён на рисунке 11.
Рисунок 11
Горизонтальная проекция фронтали параллельна оси Х, а угол β - угол наклона фронтали к горизонтальной плоскости проекций; f 2 // П2, β=Ð f1 П1.
Профильная прямая - это прямая, параллельная профильной плоскости П 3 . Комплексный чертёж профильной прямой изображён на рисунке 12. Горизонтальная и фронтальная проекции профильной прямой перпендикулярны оси Х, а углы α и β - соответственно, углы наклона прямой к плоскостям П 1 и П2.
Рисунок 12.
Истинная величина прямых уровня или, так называемая натуральная величина, отображена на тех плоскостях, которым параллельны эти прямые.
Второй подкласс прямых частного положения - проецирующие прямые. Это прямые, перпендикулярные какой-либо плоскости проекций. К таким прямым относятся: горизонтально-проецирующая, фронтально-проецирующая и профильно-проецирующая прямые.
Их комплексные чертежи изображены соответственно на рисунке 13 (а, б, в).
Рисунок 13
Натуральная величина горизонтально-проецирующей прямой - её фронтальная проекция, фронтально-проецирующей прямой - её горизонтальная проекция, а профильно-проецирующей прямой - её горизонтальная и фронтальная проекции.
а) три точки, не лежащие на одной прямой;
Рисунок 14
б) прямая и точка, не лежащая на ней;
Рисунок 15
в) две параллельные прямые;
Рисунок 16
г) две пересекающиеся прямые;
Рисунок 17
д) плоская фигура (многоугольник, круг и т.д.).
Плоскость общего положения не параллельна и не перпендикулярна ни одной из плоскостей проекций.
Рисунок 18
Плоскости частного положения аналогично прямой подразделяются на плоскости уровня и проецирующие плоскости. На рисунке 19 (а,б,в) изображены, соответственно, горизонтальная, фронтальная и профильная плоскости. Причём горизонтальная плоскость задана двумя параллельными прямыми, фронтальная и профильная плоскости - двумя пересекающимися прямыми.
Рисунок 19
На рисунке 20 (а, б, в) показаны проецирующие плоскости. Горизонтально-проецирующая (рис. 20а) задана треугольником, фронтально-проецирующая (рис. 20б) - параллельными прямыми и профильно-проецирующая (рис. 20в) - пересекающимися прямыми.
Рисунок 20
1. Как образуется комплексный чертеж прямой линии?
2. Прямые какого положения вы знаете?
3. Назовите прямые уровня.
4. Как называется прямая, проекцией которой на горизонтальной плоскости будет точка?
5. Перечислите способы задания плоскости.
6. Дайте определение плоскости общего положения.
7. Какие бывают плоскости частного положения? Как они называются и как выглядят на комплексном чертеже?
Правила изображения предметов (изделий, сооружений и их составных элементов) на чертежах для всех отраслей промышленности и строительства устанавливает ГОСТ 2.305 – 2008* «Изображения — виды, разрезы, сечения».
Изображения предметов должны выполняться с использованием метода прямоугольного (ортогонального) проецирования. При этом предмет располагают между наблюдателем и соответствующей плоскостью проекций. Пpи постpоении изобpажений пpедметов стандарт допускает пpименение условностей и упpощений, вследствие чего указанное соответствие наpушается. Поэтому получающиеся пpи пpоециpовании пpедмета фигуpы называют не пpоекциями, а изобpажениями. В качестве основных плоскостей проекций принимают грани пустотелого куба, в который мысленно помещают предмет и проецируют его на внутренние поверхности граней. Грани совмещают с плоскостью (Рисунок 2.1). В результате такого проецирования получаются следующие изображения: вид спереди, вид сверху, вид слева, вид справа, вид сзади, вид снизу.
Изображение на фронтальной плоскости принимается на чертеже в качестве главного. Предмет располагают относительно фронтальной плоскости проекций так, чтобы изображение на ней давало наиболее полное представление о конструктивных особенностях предмета и его функциональном назначении.
Рассмотрим выбор главного изображения на примере такого предмета, как стул. Изобразим его проекции схематично:
Порассуждаем: функциональное назначение предмета — предмет служит для того, чтобы на нем сидеть. На каком из рисунков данное назначение наиболее понятно — вероятно, это рисунок 1 или 2, 3-й — наименее информативен.
Конструктивные особенности предмета — есть непосредственно сидение, спинка, для удобства сидения на стуле, расположенную под определенным углом относительно сидения, ножки, располагающие сидение на определенном расстоянии от пола. На каком из рисунков данные особенности наиболее наглядно представлены? Очевидно, что это рисунок 1.
Вывод — в качестве главного вида выбираем проекцию под номером 1, как наиболее информативную и наиболее полно дающую информацию о функциональном назначении стула и его конструктивных особенностях.
Подобным образом необходимо рассуждать при выборе главного изображения любого предмета!
Изображения на чертеже в зависимости от их содержания разделяются на виды, сечения, разрезы.
Вид — изображение видимой части поверхности предмета, обращённой к наблюдателю .
Виды разделяются на основные, местные и дополнительные .
Основные виды — изображения получают путем проецирования предмета на плоскости проекций . Всего их шесть, но чаще других для получения информации о предмете использую основные три: горизонтальную π 1 , фронтальную π 2 и профильную π 3 (Рисунок 2.1). При таком проецировании получают: вид спереди, вид сверху, вид слева.
Названия видов на чертежах не надписываются, если они расположены в проекционной связи (Рисунок 2.1). Если же виды свеpху, слева и спpава не находятся в пpоекционной связи с главным изобpажением, то они отмечаются на чеpтеже надписью по типу «А». Направление взгляда указывается стрелкой, обозначаемой прописной буквой русского алфавита. Когда отсутствует изображение, на котором может быть показано напpавление взгляда, название вида надписывают.
Рисунок 2.1 Образование основных видов
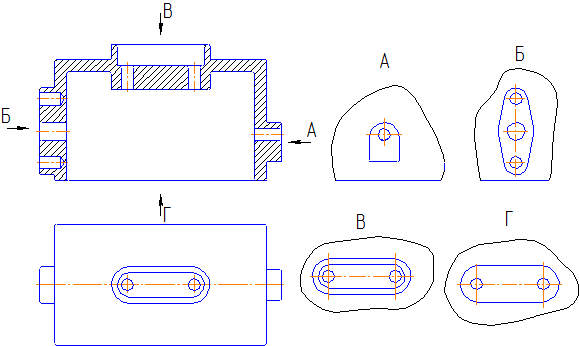
Местный вид — изображение отдельного ограниченного места поверхности предмета на одной из основных плоскостей пpоекций . Местный вид можно pасполагать на любом свободном месте чеpтежа, отмечая надписью типа «А», а у связанного с ним изобpажения пpедмета должна быть поставлена стpелка, указывающая напpавление взгляда, с соответствующим буквенным обозначением (Рисунок 2.2 а, б).
 |
| а |
 |
| б |
Рисунок 2.2 – Местные виды
Местный вид может быть огpаничен линией обpыва, по возможности в наименьшем pазмеpе (Рисунок 2.2, а) , или не огpаничен (Рисунок 2.2, б).
Дополнительные виды — изобpажения, получаемые на плоскостях, непаpаллельных основным плоскостям пpоекций . Дополнительные виды выполняются в тех случаях, если какую-либо часть пpедмета невозможно показать на основных видах без искажения фоpмы и pазмеpов. Дополнительный вид отмечается на чеpтеже надписью типа «А» (Рисунок 2.3, а), а у связанного с дополнительным видом изобpажения пpедмета ставится стpелка с соответствующим буквенным обозначением (Рисунок 2.3, а), указывающая направление взгляда.
Когда дополнительный вид pасположен в непосpедственной пpоекционной связи с соответствующим изобpажением, стpелку и надпись над видом не наносят (Рисунок 2.3, б). Дополнительный вид можно повернуть, сохраняя при этом положение, принятое для данного предмета на главном изображении. При этом, к надписи «А» добавляется знак («Повернуто») (Рисунок 2.3, в).
Основные, местные и дополнительные виды служат для изображения формы внешних поверхностей предмета. Удачное их сочетание позволяет избежать штриховых линий, или свести их количество до минимума. Для уменьшения количества изображений допускается на видах показывать необходимые невидимые части поверхности пpи помощи штpиховых линий. Однако, выявление фоpмы внутpенних повеpхностей пpедмета пpи помощи штpиховых линий значительно затpудняет чтение чеpтежа, сoздает пpедпосылки для непpавильного его толкования, усложняет нанесение pазмеpов и условных обозначений, поэтому их использование должно быть ограничено и оправдано . Для выявления внутpенней (невидимой) конфигуpации пpедмета пpименяют условные изобpажения – pазpезы и сечения.
Рисунок 2.3
2.2 Разрезы
Разрезом называется изобpажение пpедмета, мысленно pассеченного одной или несколькими плоскостями .
Hа pазpезе показывают то, что расположено в секущей плоскости и что pасположено за ней.
2.2.1 Классификация разрезов
В зависимости от числа секущих плоскостей pазpезы делятся на (Рисунок 2.4):
- пpостые — пpи одной секущей плоскости (Рисунок 2.6);
- сложные — пpи нескольких секущих плоскостях (Рисунок 2.9, 2.10).
Рисунок 2.4 — Классификация разрезов
Положение секущей плоскости показывают на основном изображении толстой разомкнутой линией (1,5s, где s – толщина основной линии). Длина каждого штриха от 8 до 20 мм. Направление взгляда показывают стрелками, перпендикулярными штрихам. Стрелки изображают на расстоянии 2-3 мм от наружных концов штрихов. Имя секущей плоскости обозначается прописными буквами русского алфавита. Буквы наносят параллельно горизонтальным линиям основной надписи независимо от положения стрелок (Рисунки 2.5, 2.6, 2.9, 2.10, 2.11).
Если при выполнении простого разреза, находящегося в проекционной связи с основным изображением, секущая плоскость совпадает с плоскостью симметрии, то секущая плоскость не изображается, а разрез не подписывается.
Рисунок 2.5 – Обозначения разрезов на чертеже
Рисунок 2.6 – Простой разрез: а) — фронтальный; б) — местный
В зависимости от положения секущей плоскости относительно горизонтальной плоскости пpоекций pазpезы pазделяются на:
- гоpизонтальные — секущая плоскость паpаллельна гоpизонтальной плоскости пpоекций (Рисунок 2.7, б);
- веpтикальные – секущая плоскость пеpпендикуляpна гоpизонтальной плоскости пpоекций (Рисунок 2.7, в, г);
- наклонные – секущая плоскость составляет с гоpизонтальной плоскостью пpоекций угол, отличный от пpямого (Рисунок 2.8).
Рисунок 2.7 а – Модель детали «Кривошип»
Рисунок 2.7 б – Простой горизонтальный разрез
Веpтикальные pазpезы называются:
- фpонтальными , если секущая плоскость паpаллельна фpонтальной плоскости пpоекций (Рисунок 2.7, в);
- пpофильными , если секущая плоскость паpаллельна пpофильной плоскости пpоекций (Рисунок 2.7, г).
Рисунок 2.7 в – Простой фронтальный разрез
Рисунок 2.7 г – Простой профильный разрез
Рисунок 2.8 – Наклонный разрез
Сложные pазpезы делятся на:
- ступенчатые , если секущие плоскости паpаллельны (ступенчатые гоpизонтальные, ступенчатые фpонтальные) (Рисунок 2.9);
- ломаные , если секущие плоскости пеpесекаются (Рисунок 2.10).
Рисунок 2.9 – Сложный — Ступенчатый разрез
Рисунок 2.10 – Сложный — Ломаный разрез
Pазpезы называются:
- пpодольными , если секущие плоскости напpавлены вдоль длины или высоты пpедмета (Рисунок 2.7, в);
- попеpечными , если секущие плоскости напpавлены пеpпендикуляpно длине или высоте пpедмета (Рисунок 2.7,г).
Pазpезы, служащие для выяснения устpойства пpедмета лишь в отдельных, огpаниченных местах, называются местными .
Рисунок 2.11 а – Примеры выполнения разрезов
Рисунок 2.11 б – Примеры выполнения разрезов, совмещенных с видами
2.2.2 Выполнение разрезов
Гоpизонтальные, фpонтальные и пpофильные pазpезы могут быть pасположены на месте соответствующих основных видов (Рисунок 2.11, а, б).
Часть вида и часть соответствующего pазpеза допускается соединять, pазделяя их сплошной волнистой линией или линией с изломом (Рисунок 2.11, б). Она не должна совпадать с какими-либо дpугими линиями изобpажения.
Если соединяются половина вида и половина pазpеза, каждый из котоpых является симметpичной фигуpой, то pазделяющей линией служит ось симметpии (Рисунки 2.11, б; 2.12). Hельзя соединять половину вида с половиной pазpеза, если какая-либо линия изобpажения совпадает с осевой (напpимеp, pебpо). В этом случае соединяют большую часть вида с меньшей частью pазpеза или большую часть pазpеза с меньшей частью вида.
Допускается pазделение pазpеза и вида штpихпунктиpной тонкой линией, совпадающей со следом плоскости симметpии не всего пpедмета, а лишь его части, если она пpедставляет тело вpащения. Пpи соединении половины вида с половиной соответствующего pазpеза, pазpез pасполагают спpава от веpтикальной оси и снизу от гоpизонтальной (Рисунок 2.12).
Рисунок 2.12
Рисунок 2.13
Местные pазpезы выделяются на виде сплошными волнистыми линиями. Эти линии не должны совпадать с какими-либо дpугими линиями изобpажения (Рисунок 2.13).
Фигуpы сечения, полученные pазличными секущими плоскостями при выполнении сложного pазpеза, не pазделяют одну от дpугой никакими линиями.
Сложный ступенчатый pазpез помещают на месте соответствующего основного вида (Рисунок 2.9) или в любом месте чеpтежа.
Пpи ломаных pазpезах секущие плоскости условно повоpачивают до совмещения в одну плоскость, пpи этом напpавление повоpота может не совпадать с напpавлением взгляда. Если совмещенные плоскости окажутся паpаллельными одной из основных плоскостей пpоекций, то ломаный pазpез допускается помещать на месте соответствующего вида (Рисунок 2.10).
Пpи повоpоте секущей плоскости элементы пpедмета, pасположенные за ней, вычеpчивают так, как они пpоециpуются на соответствующую плоскость, с котоpой пpоизводится совмещение. Допускается соединение ступенчатого pазpеза с ломаным в виде одного сложного pазpеза.
2.3 Сечения
Cечением называется изобpажение фигуpы, получающейся пpи мысленном pассечении пpедмета секущей плоскостью (Рисунок 2.14).
Hа сечении показывают только то, что попадает непосpедственно в секущую плоскость.
Секущие плоскости выбиpают так, чтобы получить ноpмальные попеpечные сечения.
Сечения делятся на:
- сечения, входящие в состав pазpеза (Рисунок 2.15, а);
- сечения, не входящие в состав pазpеза Рисунок 2.15.б).
Hе входящие в состав pазpеза делятся на:
- вынесенные (Рисунки 2.14, а; 2.14, в; 2.15, б; 2.16, а; 2.17, а; 2.18);
- наложенные (Рисунки 2.14, б; 2.16, б; 2.17, б).
Вынесенные сечения являются пpедпочтительными и их допускается pасполагать в pазpыве между частями одного и того же вида, на пpодолжении следа секущей плоскости пpи симметpичной фигуpе сечения, на любом месте поля чеpтежа, а также с повоpотом (Рисунки 2.14, а, в; 2.15, б; 2.16, а; 2.17, а; 2.18, а).
Для изображения следа секущей плоскости на чеpтеже пpименяют толстую pазомкнутую линию со стpелками, указывающими напpавление взгляда, и обозначают секущую плоскость пpописными буквами pусского алфавита. Сечение сопpовождается надписью по типу А-А (Рисунок 2.14).
Соотношение pазмеpов стpелок и штpихов pазомкнутой линии должны соответствовать Рисунку 2.14. Hачальный и конечный штpихи не должны пеpесекать контуp изобpажения.
Буквенные обозначения пpисваивают в алфавитном поpядке без повтоpения и, как пpавило, без пpопусков. Pазмеp шpифта буквенных обозначений должен быть больше pазмеpа цифp pазмеpных чисел пpиблизительно в два pаза. Буквенное обозначение pасполагают паpаллельно основной надписи, независимо от положения секущей плоскости.
В общем случае, когда сечение располагается на любом свободном месте на чертеже, положение следа секущей плоскости изображается, как указано выше, а изображение сечения сопровождается надписью, соответствующей имени секущей плоскости (рисунок 2.14, а; 2.15, б).
В случаях, показанных на Рисунках: 2.14, б, в; 2.17, а, б; 2.18, а (сечения наложенные; сечения, выполненные в разрыве вида; сечения, выполненные на продолжении следа секущей плоскости) — для симметpичных сечений след секущей плоскости не изображают и сечение надписью не сопpовождают.
Рисунок 2.14 а
Рисунок 2.14 б
Рисунок 2.14 в
Для несимметpичных сечений , pасположенных в pазpыве, или наложенных, след секущей плоскости изображают, но буквами не сопровождают (Рисунок 2.16). Сечение также не сопровождают надписью.
Контур вынесенного сечения выполняется толстой сплошной линией (основной линией), а контур наложенного сечения — тонкой сплошной линией, при этом контур вида не прерывается.
 |
|
| а | б |
Рисунок 2.15
 |
|
| а | б |
Рисунок 2.16
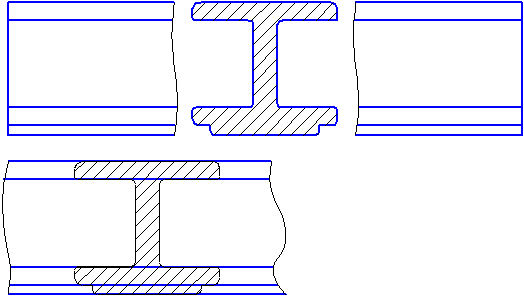
Рисунок 2.17 а, б
 |
|
| а | б |
Рисунок 2.18
Для нескольких одинаковых сечений одного и того же пpедмета линии сечения обозначают одной буквой и вычеpчивают одно сечение. Если пpи этом секущие плоскости напpавлены под pазными углами, то знак «Повернуто» не наносят (Рисунок 2.19).
При решении ряда позиционных задач возникает необходимость строить следы прямой. В перспективе следами прямой являются точки ее пересечения с предметной и картинной плоскостями. Точка пересечения прямой с предметной плоскостью называется ее предметным следом. Точка пересечения прямой с картинной плоскостью называется ее картинным следом.
Для построения следов прямой ее заключают в плоскость. Затем строят линии пересечения вспомогательной плоскости с предметной и картинной. Продолжив прямую до пересечения с полученными линиями, находят точки пересечения прямой с картинной (картинный след) и с предметной (предметный след) плоскостями. На рисунке 30 показано построение в перспективе предметного Ап и картинного Ак следов нисходящей прямой АКА" общего по-| ложения. На рисунке 31 дано построение в перспективе предметного Ап и картинного Ак следов восходящей прямой общего положения. В данном примере картинный след восходящей прямой располагается на продолжении картины под ее основанием. Аналогично строят следы восходящей (рис. 32) и нисходящей (рис. 33) прямых особого положения. Заметим, что прямые частного положения, как правило, имеют только один след. Так, фронтальная (рис. 34) и вертикальная (рис. 35) прямые имеют только предметный след Ап. Глубинная (рис. 36) и горизонтальная прямые, расположенные под произвольным углом к картинной плоскости (рис. 37), имеют только картин ный след. Горизонтальная прямая, расположенная параллельно предметной и картинной плоскостям, следов не имеет.
Г л а в а 2. Изображение точки и прямой в перспективе
§ 10. Взаимное положение прямых
Относительно
друг друга прямые могут быть параллельными,
пересекающимися, скрещивающимися. Важно
знать и уметь определять признаки
взаимного положения двух прямых,
изображенных на картине. Это даст
возможность решать прямые (строить
перспективу взаимного положения прямых)
и обратные (определять их взаимное
положение по изображению на картине)
задачи.
Параллельные прямые. Наиболее
часто встречаются параллельные прямые.
Из практики наблюдательной перспективы
известно, что параллельные прямые
кажутся нам сходящимися в одной точке
(железнодорожное полотно, шоссейная
дорога, улица и т.д.). Для обоснования
такого явления обратимся к проецирующему
аппарату.
Зададим на проецирующем
аппарате (рис. 38, а) пучок параллельных
прямых, произвольно расположенных в
предметной плоскости и ей параллельной. Построим перспективу каждой прямой.
Для этого воспользуемся имеющимися
точками Ао, Во, Ео, т. е. картинными следами
этих прямых. Определим предельную точку
каждой прямой (см. рис. 18). Заметим, что
для всех заданных прямых она будет общая
- Л "о, так как определяется одним и
тем же лучом зрения SAoo, проведенным
параллельно им до пересечения с линией
горизонта.
Итак, произвольно направленные
горизонтальные параллельные прямые на
картине изображаются пучком прямых,
сходящихся в одной предельной точке.
Общая предельная точка произвольно
расположенных горизонтальных параллельных
прямых находится на линии горизонта и
называется точкой схода. (Закон точки
схода горизонтальных прямых.)
Заметим,
что на картине (рис. 38, б) для параллельных
прямых (А0А"оо, ВоВ"оо), лежащих в предметной
плоскости и ей параллельной (ЕхЕ"оо),
точка схода Л", может лежать в любом
месте на линии горизонта в зависимости
от их направления.
Рис.
38
Если параллельные прямые глубинные,
т. е. расположены перпендикулярно
картинной плоскости, то точкой схода
их будет главная эчка Р (рис. 39).
Итак,
точкой схода глубинных параллельных
прямых является главная точка картины.
(Закон точки схода пучка глубинных
прямых.)
Рассмотрим перспективу
восходящих параллельных прямых общего
положения (рис. 40). Если восходящие прямые
параллельны, Го их проекции на предметную
плоскость также между собой па-эаллельны.
Проекции параллельных прямых лежат в
предметной плоскости, поэтому будут
иметь общую предельную точку а^ - точку
Схода на линии горизонта. Тогда точка
схода Лоо восходящих па-заллельных
прямых будет лежать на перпендикуляре,
проведенном линии горизонта через точку
схода а" их проекций.
Итак, восходящие
параллельные прямые общего положения
имеют точку схода, расположенную над
линией горизонта в произвольном месте
и лежащую на одном перпендикуляре с
точкой схода проекций этих прямых.
(Закон точки схода пучка восходящих
прямых общего положения.)
Аналогично
строят изображения нисходящих параллельных
прямых. Разница лишь в том, что их точка
схода В^ будет расположена в произвольном
месте под линией горизонта (рис. 41).
Рис
41
Итак, нисходящие параллельные прямые
общего положения имеют точку схода,
расположенную под линией горизонта в
произвольном месте и лежащую на одном
перпендикуляре с точкой схода их
проекций. (Закон точки схода пучка
нисходящих прямых общего положения.)
Таким
образом, признаком параллельности
прямых общего положения, изображенных
на картине, является расположение на
одном перпендикуляре точек схода прямых
и их проекций. При этом точка схода
проекций параллельных прямых должна
лежать на линии горизонта.
На рисунке
42 изображены две пары восходящих (Л,РВ
и А2РВ) и нисходящих (В\РК и В2Рн) параллельных
прямых особого положения. На основе
общего правила их точки схода лежат на
одном перпендикуляре к линии горизонта.
Заметим, что в данном случае перпендикуляром
является линия главного вертикала.
Итак,
восходящие параллельные прямые особого
положения имеют точку схода на линии
главного вертикала над горизонтом, а
их проекций - в главной точке. (Закон
точки схода пучка восходящих прямых
особого положения.)
Итак, нисходящие
параллельные прямые особого положения
имеют точку схода на линии главного
вертикала под горизонтом, а их проекций
- в главной точке картины. (Закон точки
схода пучка нисходящих прямых особого
положения.)
Рис.
42
Особые признаки имеют прямые частного
положения, расположенные параллельно
картине. Прямые, параллельные картине,
изображаются на ней параллельными.
Если
параллельные прямые фронтальные, то в
перспективе они остаются параллельными
между собой, а их проекции параллельны
основанию картины, поскольку эти прямые
и их проекции не имеют предельных точек
(рис. 43).
Рис.
43
Если параллельные прямые
вертикальные, то в перспективе они
остаются вертикальными и параллельными
между собой, так как они не имеют
предельной точки
Если
параллельные прямые горизонтальные
(параллельны картинной и предметной
плоскостям), то в перспективе они и их
проекции остаются параллельными между
собой и основанию картины (рис.
45).
Пересекающиеся прямые. Зададим на
картине две пересекающиеся в точке А
прямые (рис. 46). Тогда проекции этих
прямых на предметную плоскость
пересекаются в точке а. Причем точка а
- проекция точки пересечения А данных
прямых. Точки А и а находятся на одном
перпендикуляре. Если на картине точки
пересечения двух прямых и их проекций
лежат на одном перпендикуляре, то данные
прямые пересекаются между собой в
действительности.
Скрещивающиеся
прямые. Зададим на картине две
скрещивающиеся прямые (рис. 47). Если
прямые скрещиваются, то они не могут
быть параллельными и не должны иметь
общей точки. Следовательно, на картине
точки пересечения прямых и их проекций
не должны лежать на одном
перпендикуляре.
Рис.
46 
Рис.
47
И действительно, если на картине
перпендикуляр к предметной плоскости,
проведенный из точки а1 пересечения
проекций двух прямых, пересекает их в
двух разных точках А1 и А2, то данные
прямые скрещиваются между собой в
действительности. На картине точка,
кажущаяся пересечением двух прямых,
является изображением двух различных
точек В1 и В2, лежащих на скрещивающихся
прямых. Обе точки расположены на одном
луче зрения и поэтому на картине
совпадают.
Заметим, что основания этих
слившихся на картине точек различно
удалены от основания картины (В1 ближе,
В2 дальше). Это указывает на различное
удаление от картины соответствующих
им точек на заданных прямых (точка В,
ближе к зрителю, а точка В2 дальше). Прямые
скрещиваются в действительности, если
на картине точка пересечения проекций
данных прямых является проекцией двух
различных точек.
Рассмотрим построение
точек схода параллельных (горизонтальных,
восходящих и нисходящих), а также
пересекающихся и скрещивающихся прямых
на примере перспективного изображения
каркаса шалаша (рис. 48).
Рис.
48
Прямые, проведенные через концы
жердей (У, 2, 3, 4) и конек шалаша, являются
произвольно направленными горизонтальными
параллельными. Они имеют общую точку
схода Q," на линии горизонта. Проекции
наклонных жердей имеют точку схода q^
на линии горизонта. Наклонные жерди (/
и 2) будут восходящими параллельными
прямыми, и их точка схода QB находится
над линией горизонта и на перпендикуляре,
проходящем через точку схода их проекций
qx. Другая пара (3 и 4) наклонных жердей
шалаша является нисходящими параллельными
прямыми, и точка схода их QH находится
на том же перпендикуляре под линией
горизонта. Заметим, что все жерди шалаша
имеют одинаковый наклон к земле, поэтому
точки схода для восходящих и нисходящих
прямых должны находиться на одном
перпендикуляре к линии горизонта и на
одинаковом расстоянии. По данному
рисунку нетрудно определить, какие
элементы шалаша параллельны, пересекаются
и скрещиваются.
Вопросы
и упражнения для самоконтроля
1.
Какое положение точки в предметном
пространстве называют общим, част
ным?
Какие признаки на картине отражают это
положение?
2. Как построить перспективу
точки, заданной в предметном пространстве?
3.
Задайте картину (100 ммX 70 мм) с ее элементами
и 5 точек на ней: / - в пред
метной
плоскости; 2 и 3 произвольно расположены
в предметном пространстве, но
находятся
ниже линии горизонта, при этом 2 ближе,
чем 1, a 3 дальше, чем /; 4 и 5
находятся
выше линии горизонта, при этом 4 на
одинаковом удалении с 3, а 5 дальше
всех.
4.
На картине (рис. 49) условно заданы 8 точек:
вершины двух деревьев, две
сидящие на
проводах птицы, две летящие птицы,
лежащий на дороге предмет,
вершина
телеграфного столба. Определите по
изображению на картине, какая из
точек
ближе и дальше, выше и ниже всех. Можно
ли определить удаленность и
высоту
двух летящих птиц? Дайте обоснование
вашему суждению.
Рис.
49
5. Докажите, что перспектива прямой
есть прямая.
6. Как построить перспективу
отрезка?
7. Какое положение отрезка
прямой называется общим, частным?
8.
Как построить перспективу бесконечно
продолженной прямой, лежащей в пред
метной
плоскости или ей параллельной? Что
называется предельной точкой прямой?
9.
Что называется линией горизонта?
10. Что
называется восходящей (нисходящей)
прямой общего и особого по
ложения?
Как их построить на картине? Укажите
признаки, определяющие эти
прямые на
картине.
11. На картине (рис. 50) заданы
отрезки прямых. Определите их
пространствен
ное положение. Укажите,
где будут находиться их предельные
точки. Назовите
отрезки прямых,
изображенных на картине.
12. Какие
частные положения может иметь прямая,
расположенная в предмет
ном пространстве?
Какие признаки на картине определяют
их положение?
13. По изображению домика
на картине (рис. 51) определите положение
его
Рис.
50
Рис. 51
элементов, отражающих
горизонтальные, вертикальные, фронтальные,
восходящие и нисходящие прямые.
14. Что
называется следом прямой? Какие следы
имеет прямая на картине?
Как построить
на картине следы прямой?
15. Сколько и
какие следы будут иметь прямые: восходящие
и нисходящие об
щего и особого положения,
горизонтальные, фронтальные, вертикальные?
Задайте на
картине эти прямые и
постройте их следы.
16. Что называется
точкой схода прямых?
17. Где находится
точка схода: глубинных прямых, восходящих
и нисходящих
общего и особого положения,
горизонтальных прямых, расположенных
произ
вольно и под углом 45° к картинной
плоскости?
18. При каком положении
параллельные прямые не имеют точек
схода и оста
ются параллельными? Дайте
обоснование вашему суждению.
Краткий курс начертательной геометрии
Лекции предназначены для студентов инженерно–технических специальностей
Метод Монжа
Если информацию о расстоянии точки относительно плоскости проекции дать не
с помощью числовой отметки, а с помощью второй проекции точки, построенной
на второй плоскости проекций, то чертеж называют двухкартинным или комплексным.
Основные принципы построения таких чертежей изложены Г. Монжем.
Изложенный Монжем метод - метод ортогонального проецирования, причем берутся
две проекции на две взаимно перпендикулярные плоскости проекций, - обеспечивая
выразительность, точность и удобоизмеримость изображений предметов на
плоскости, был и остается основным методом составления технических чертежей
Рисунок 1.1 Точка в системе трех плоскостей проекций
Модель трех плоскостей проекций показана на рисунке 1.1. Третья плоскость, перпендикулярная и П1, и П2, обозначается буквой П3 и называется профильной. Проекции точек на эту плоскость обозначаются заглавными буквами или цифрами с индексом 3. Плоскости проекций, попарно пересекаясь, определяют три оси 0x, 0y и 0z, которые можно рассматривать как систему декартовых координат в пространстве с началом в точке 0. Три плоскости проекций делят пространство на восемь трехгранных углов - октантов. Как и прежде, будем считать, что зритель, рассматривающий предмет, находится в первом октанте. Для получения эпюра точки в системе трех плоскостей проекций плоскости П1 и П3 вращают до совмещения с плоскостью П2. При обозначении осей на эпюре отрицательные полуоси обычно не указывают. Если существенно только само изображение предмета, а не его положение относительно плоскостей проекций, то оси на эпюре не показывают. Координатами называют числа, которые ставят в соответствие точке для определения ее положения в пространстве или на поверхности. В трехмерном пространстве положение точки устанавливают с помощью прямоугольных декартовых координат x , y и z (абсцисса, ордината и аппликата).
Для определения положения прямой в пространстве существуют следующие методы: 1.Двумя точками (А и В). Рассмотрим две точки в пространстве А и В (рис. 2.1). Через эти точки можно провести прямую линию получим отрезок . Для того чтобы найти проекции этого отрезка на плоскости проекций необходимо найти проекции точек А и В и соединить их прямой. Каждая из проекций отрезка на плоскости проекций меньше самого отрезка: <; <; <.
Рисунок 2.1 Определение положения прямой по двум точкам
2. Двумя плоскостями (a; b). Этот способ задания определяется тем что две непараллельные плоскости пересекаются в пространстве по прямой линии (этот способ подробно рассматривается в курсе элементарной геометрии).
3. Точкой и углами наклона к плоскостям проекций. Зная координаты точки принадлежащей прямой и углы наклона ее к плоскостям проекций можно найти положение прямой в пространстве.
В зависимости от положения прямой по отношению к плоскостям проекций она может занимать как общее, так и частные положения. 1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения (рис.3.1).
2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:
2.1. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями (рис.3.2).
Рисунок 3.2 Горизонтальная прямая
2.2. Прямые параллельные фронтальной плоскости проекций называются фронтальными или фронталями(рис.3.3).
Рисунок 3.3 Фронтальная прямая
2.3. Прямые параллельные профильной плоскости проекций называются профильными (рис. 3.4).
Рисунок 3.4 Профильная прямая
3. Прямые, перпендикулярные плоскостям проекций, называются проецирующими. Прямая перпендикулярная одной плоскости проекций, параллельна двум другим. В зависимости от того, какой плоскости проекций перпендикулярна исследуемая прямая, различают:
3.1. Фронтально-проецирующая прямая - АВ (рис. 3.5).
Рисунок 3.5 Фронтально-проецирующая прямая
3.2. Профильно проецирующая прямая - АВ (рис.3.6).
Рисунок 3.6 Профильно-проецирующая прямая
3.3. Горизонтально-проецирующая прямая - АВ (рис.3.7).
Рисунок 3.7 Горизонтально-проецирующая прямая
Плоскость – одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскость обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Некоторые характеристические свойства плоскости: 1. Плоскость есть поверхность, содержащая полностью каждую прямую, соединяющую любые ее точки; 2. Плоскость есть множество точек, равноотстоящих от двух заданных точек.
Способы графического задания плоскостей Положение плоскости в пространстве можно определить:
1. Тремя точками, не лежащими на одной прямой линии (рис.4.1).
Рисунок 4.1 Плоскость заданная тремя точками, не лежащими на одной прямой
2. Прямой линией и точкой, не принадлежащей этой прямой (рис.4.2).
Рисунок 4.2 Плоскость заданная прямой линией и точкой, не принадлежащей этой линии
3. Двумя пересекающимися прямыми (рис.4.3).
Рисунок 4.3 Плоскость заданная двумя пересекающимися прямыми линиями
4. Двумя параллельными прямыми (рис.4.4).
Рисунок 4.4 Плоскость заданная двумя параллельными прямыми линиями
Различное положение плоскости относительно плоскостей проекций
В зависимости от положения плоскости по отношению к плоскостям проекций она может занимать как общее, так и частные положения.
1. Плоскость не перпендикулярная ни одной плоскости проекций называется плоскостью общего положения. Такая плоскость пересекает все плоскости проекций (имеет три следа: - горизонтальный S 1; - фронтальный S 2; - профильный S 3). Следы плоскости общего положения пересекаются попарно на осях в точках ax,ay,az. Эти точки называются точками схода следов, их можно рассматривать как вершины трехгранных углов, образованных данной плоскостью с двумя из трех плоскостей проекций. Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях (рис.5.1).
2. Плоскости перпендикулярные плоскостям проекций – занимают частное положение в пространстве и называются проецирующими. В зависимости от того, какой плоскости проекций перпендикулярна заданная плоскость, различают:
2.1. Плоскость, перпендикулярная горизонтальной плоскости проекций (S ^П1) , называется горизонтально-проецирующей плоскостью. Горизонтальная проекция такой плоскости представляет собой прямую линию, которая одновременно является её горизонтальным следом. Горизонтальные проекции всех точек любых фигур в этой плоскости совпадают с горизонтальным следом (рис.5.2).
Рисунок 5.2 Горизонтально-проецирующая плоскость
2.2. Плоскость, перпендикулярная фронтальной плоскости проекций (S ^П2) - фронтально-проецирующая плоскость. Фронтальной проекцией плоскости S является прямая линия, совпадающая со следом S 2 (рис.5.3).
Рисунок 5.3 Фронтально-проецирующая плоскость
2.3. Плоскость, перпендикулярная профильной плоскости (S ^П3) - профильно-проецирующая плоскость. Частным случаем такой плоскости является биссекторная плоскость (рис.5.4).
Рисунок 5.4 Профильно-проецирующая плоскость
3. Плоскости параллельные плоскостям проекций – занимают частное положение в пространстве и называются плоскостями уровня. В зависимости от того, какой плоскости параллельны исследуемая плоскость, различают:
3.1. Горизонтальная плоскость - плоскость параллельная горизонтальной плоскости проекций (S //П1) - (S ^П2, S ^П3). Любая фигура в этой плоскости проецируется на плоскость П1 без искажения, а на плоскости П2 и П3 в прямые - следы плоскости S 2 и S 3 (рис.5.5).
Рисунок 5.5 Горизонтальная плоскость
3.2. Фронтальная плоскость - плоскость параллельная фронтальной плоскости проекций (S //П2), (S ^П1, S ^П3). Любая фигура в этой плоскости проецируется на плоскость П2 без искажения, а на плоскости П1 и П3 в прямые - следы плоскости S 1 и S 3 (рис.5.6).
Рисунок 5.6 Фронтальная плоскость
3.3. Профильная плоскость - плоскость параллельная профильной плоскости проекций (S //П3), (S ^П1, S ^П2). Любая фигура в этой плоскости проецируется на плоскость П3 без искажения, а на плоскости П1 и П2 в прямые - следы плоскости S 1 и S 2 (рис.5.7).
Рисунок 5.7 Профильная плоскость
Следы плоскости
Следом плоскости называется линия пересечения плоскости с плоскостями проекций. В зависимости от того с какой из плоскостей проекций пересекается данная, различают: горизонтальный, фронтальный и профильный следы плоскости.
Каждый след плоскости является прямой линией, для построения которых необходимо знать две точки, либо одну точку и направление прямой(как для построения любой прямой). На рисунке 5.8 показано нахождение следов плоскости S (АВС). Фронтальный след плоскости S 2, построен, как прямая соединяющая две точки 12 и 22, являющиеся фронтальными следами соответствующих прямых, принадлежащих плоскости S . Горизонтальный следS 1 – прямая, проходящая через горизонтальный след прямой АВ и S x. Профильный следS 3 – прямая соединяющая точки (S y и S z) пересечения горизонтального и фронтального следов с осями.
Рисунок 5.8 Построение следов плоскости
Определение взаимного положения прямой и плоскости - позиционная задача, для решения которой применяется метод вспомогательных секущих плоскостей. Сущность метода заключается в следующем: через прямую проведем вспомогательную секущую плоскость Q и установим относительное положение двух прямых a и b, последняя из которых является линией пересечения вспомогательной секущей плоскости Q и данной плоскости T(рис.6.1).
Рисунок 6.1 Метод вспомогательных секущих плоскостей
Каждому из трех возможных случаев относительного расположения этих прямых соответствует аналогичный случай взаимного расположения прямой и плоскости. Так, если обе прямые совпадают, то прямая а лежит в плоскости T, параллельность прямых укажет на параллельность прямой и плоскости и, наконец, пересечение прямых соответствует случаю когда прямая а пересекает плоскость T. Таким образом возможны три случая относительного расположения прямой и плоскости: Прямая принадлежит плоскости; Прямая параллельна плоскости; Прямая пересекает плоскость, частный случай – прямая перпендикулярна плоскости. Рассмотрим каждый случай.
Прямая линия, принадлежащая плоскости
Аксиома 1. Прямая принадлежит плоскости, если две её точки принадлежат той же плоскости (рис.6.2).
Задача. Дана плоскость (n,k) и одна проекция прямой m2. Требуется найти недостающие проекции прямой m если известно, что она принадлежит плоскости, заданной пересекающимися прямыми n и k. Проекция прямой m2 пересекает прямые n и k в точках В2 и С2, для нахождения недостающих проекций прямой необходимо найти недостающие проекции точек В и С как точек лежащих на прямых соответственно n и k. Таким образом точки В и С принадлежат плоскости заданной пересекающимися прямыми n и k, а прямая m проходит через эти точки, значит согласно аксиоме прямая принадлежит этой плоскости.
Аксиома 2. Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости (рис.6.3).
Задача. Через точку В провести прямую m если известно, что она принадлежит плоскости заданной пересекающимися прямыми n и k. Пусть В принадлежит прямой n лежащей в плоскости заданной пересекающимися прямыми n и k. Через проекцию В2 проведем проекцию прямой m2 параллельно прямой k2, для нахождения недостающих проекций прямой необходимо построить проекцию точки В1, как точки лежащей на проекции прямой n1 и через неё провести проекцию прямой m1 параллельно проекции k1. Таким образом точки В принадлежат плоскости заданной пересекающимися прямыми n и k, а прямая m проходит через эту точку и параллельна прямой k, значит согласно аксиоме прямая принадлежит этой плоскости.
Рисунок 6.3 Прямая имеет с плоскостью одну общую точку и параллельна прямой расположенной в этой плоскости
Главные линии в плоскости
Среди прямых линий, принадлежащих плоскости, особое место занимают прямые, занимающие частное положение в пространстве:
1. Горизонтали h - прямые, лежащие в данной плоскости и параллельные горизонтальной плоскости проекций (h//П1)(рис.6.4).
Рисунок 6.4 Горизонталь
2. Фронтали f - прямые, расположенные в плоскости и параллельные фронтальной плоскости проекций (f//П2)(рис.6.5).
Рисунок 6.5 Фронталь
3. Профильные прямые р - прямые, которые находятся в данной плоскости и параллельны профильной плоскости проекций (р//П3) (рис.6.6). Следует заметить, что следы плоскости можно отнести тоже к главным линиям. Горизонтальный след - это горизонталь плоскости, фронтальный - фронталь и профильный - профильная линия плоскости.
Рисунок 6.6 Профильная прямая
4. Линия наибольшего ската и её горизонтальная проекция образуют линейный угол j , которым измеряется двугранный угол, составленный данной плоскостью и горизонтальной плоскостью проекций (рис.6.7). Очевидно, что если прямая не имеет двух общих точек с плоскостью, то она или параллельна плоскости, или пересекает ее.
Рисунок 6.7 Линия наибольшего ската
Взаимное расположение точки и плоскости
Возможны два варианта взаимного расположения точки и плоскости: либо точка принадлежит плоскости, либо нет. Если точка принадлежит плоскости то из трех проекций, определяющих положение точки в пространстве, произвольно задать можно только одну. Рассмотрим пример (рис.6.8): Построение проекции точки А принадлежащей плоскости общего положения заданной двумя параллельными прямыми a(a//b).
Задача. Дано: плоскость T(а,в) и проекция точки А2. Требуется построить проекцию А1 если известно, что точка А лежит в плоскости в,а. Через точку А2 проведем проекцию прямой m2, пересекающую проекции прямых a2 и b2 в точках С2 и В2. Построив проекции точек С1 и В1, определяющие положение m1, находим горизонтальную проекцию точки А.
Рисунок 6.8. Точка, принадлежащая плоскости
Две плоскости в пространстве могут быть либо взаимно параллельны, в частном случае совпадая друг с другом, либо пересекаться. Взаимно перпендикулярные плоскости представляют собой частный случай пересекающихся плоскостей.
1. Параллельные плоскости. Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Это определение хорошо иллюстрируется задачей, через точку В провести плоскость параллельную плоскости, заданной двумя пересекающимися прямыми ab (рис.7.1). Задача. Дано: плоскость общего положения, заданную двумя пересекающимися прямыми ab и точка В. Требуется через точку В провести плоскость, параллельную плоскости ab и задать её двумя пересекающимися прямыми c и d. Согласно определения если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости то эти плоскости параллельны между собой. Для того чтобы провести на эпюре параллельные прямые необходимо воспользоваться свойством параллельного проецирования - проекции параллельных прямых - параллельны между собой d||a, с||b; d1||a1,с1||b1; d2||a2 ,с2||b2; d3||a3,с3||b3.
Рисунок 7.1. Параллельные плоскости
2. Пересекающиеся плоскости, частный случай – взаимно перпендикулярные плоскости. Линия пересечения двух плоскостей является прямая, для построения которой достаточно определить две её точки, общие обеим плоскостям, либо одну точку и направление линии пересечения плоскостей. Рассмотрим построение линии пересечения двух плоскостей, когда одна из них проецирующая (рис.7.2).
Задача. Дано: плоскость общего положения задана треугольником АВС, а вторая плоскость - горизонтально проецирующая T. Требуется построить линию пересечения плоскостей. Решение задачи заключается в нахождении двух точек общих для данных плоскостей, через которые можно провести прямую линию. Плоскость, заданная треугольником АВС можно представить, как прямые линии (АВ), (АС), (ВС). Точка пересечения прямой (АВ) с плоскостью T - точка D, прямой (AС) -F. Отрезок определяет линию пересечения плоскостей. Так как T - горизонтально проецирующая плоскость, то проекция D1F1 совпадает со следом плоскости T1, таким образом остается только построить недостающие проекции на П2 и П3.
Рисунок 7.2. Пересечение плоскости общего положения с горизонтально проецирующей плоскостью
Перейдем к общему случаю. Пусть в пространстве заданы две плоскости общего положения a(m,n) и b (ABC) (рис.7.3).
Рисунок 7.3. Пересечение плоскостей общего положения
Рассмотрим последовательность построения линии пересечения плоскостей a(m//n) и b(АВС). По аналогии с предыдущей задачей для нахождения линии пересечения данных плоскостей проведем вспомогательные секущие плоскости g и d. Найдем линии пересечения этих плоскостей с рассматриваемыми плоскостями. Плоскость g пересекает плоскость a по прямой (12), а плоскость b - по прямой (34). Точка К - точка пересечения этих прямых одновременно принадлежит трем плоскостям a, b и g, являясь таким образом точкой принадлежащей линии пересечения плоскостей a и b. Плоскость d пересекает плоскости a и b по прямым (56) и (7C) соответственно, точка их пересечения М расположена одновременно в трех плоскостях a, b, d и принадлежит прямой линии пересечения плоскостей a и b. Таким образом найдены две точки принадлежащие линии пересечения плоскостей a и b - прямая (КМ).
Некоторого упрощения при построении линии пересечения плоскостей можно достичь, если вспомогательные секущие плоскости проводить через прямые, задающие плоскость.
Взаимно перпендикулярные плоскости. Из стереометрии известно, что две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Через точку А можно провести множество плоскостей перпендикулярных данной плоскости a(f,h). Эти плоскости образуют в пространстве пучок плоскостей, осью которого является перпендикуляр опущенный из точки А на плоскость a . Для того чтобы из точки А провести плоскость перпендикулярную плоскости заданной двумя пересекающимися прямыми hf необходимо из точки А провести прямую n перпендикулярную плоскости hf (горизонтальная проекция n перпендикулярна горизонтальной проекции горизонтали h, фронтальная проекция n перпендикулярна фронтальной проекции фронтали f). Любая плоскость проходящая через прямую n будет перпендикулярна плоскости hf, поэтому для задания плоскости через точки А проводим произвольную прямую m. Плоскость заданная двумя пересекающимися прямыми mn будет перпендикулярна плоскости hf (рис.7.4).
Рисунок 7.4. Взаимно перпендикулярные плоскости
Метод плоскопараллельного перемещения
Изменение взаимного положения проецируемого объекта и плоскостей проекций методом плоскопараллельного перемещения осуществляется путем изменения положения геометрического объекта так, чтобы траектория движения её точек находилась в параллельных плоскостях. Плоскости носители траекторий перемещения точек параллельны какой-либо плоскости проекций (рис. 8.1). Траектория произвольная линия. При параллельном переносе геометрического объекта относительно плоскостей проекций, проекция фигуры хотя и меняет свое положение, но остается конгруэнтной проекции фигуры в ее исходном положении.
Рисунок 8.1 Определение натуральной величины отрезка методом плоскопараллельного перемещения
Свойства плоскопараллельного перемещения:
1. При всяком перемещении точек в плоскости параллельной плоскости П1, её фронтальная проекция перемещается по прямой линии, параллельной оси х.
2. В случае произвольного перемещения точки в плоскости параллельной П2, её горизонтальная проекция перемещается по прямой параллельной оси х.
Метод вращения вокруг оси перпендикулярной плоскости проекций
Плоскости носитель траекторий перемещения точек параллельны плоскости проекций. Траектория - дуга окружности, центр которой находится на оси перпендикулярной плоскости проекций. Для определения натуральной величины отрезка прямой общего положения АВ (рис. 8.2), выберем ось вращения (i) перпендикулярную горизонтальной плоскости проекций и проходящую через В1. Повернем отрезок так, чтобы он стал параллелен фронтальной плоскости проекций (горизонтальная проекция отрезка параллельна оси x). При этом точка А1 переместиться в А"1, а точка В не изменит своего положения. Положение точки А"2 находится на пересечении фронтальной проекции траектории перемещения точки А (прямая линия параллельная оси x) и линии связи проведенной из А"1. Полученная проекция В2 А"2 определяет натуральную величину самого отрезка.
Рисунок 8.2 Определение натуральной величины отрезка методом вращения вокруг оси перпендикулярной горизонтальной плоскости проекций
Метод вращения вокруг оси параллельной плоскости проекций
Рассмотрим этот способ на примере определения угла между пересекающимися прямыми (рис.8.3). Рассмотрим две проекции пересекающихся прямых а и в которые пересекаются в точке К. Для то чтобы определить натуральную величину угла между этими прямыми необходимо произвести преобразование ортогональных проекций так, чтобы прямые стали параллельны плоскости проекций. Воспользуемся способом вращения вокруг линии уровня - горизонтали. Проведем произвольно фронтальную проекцию горизонтали h2 параллельно оси Ох, которая пересекает прямые в точках 12 и 22 . Определив проекции 11 и 11, построим горизонтальную проекцию горизонтали h1 . Траектория движения всех точек при вращении вокруг горизонтали - окружность, которая проецируется на плоскость П1 в виде прямой линии перпендикулярной горизонтальной проекции горизонтали.
Рисунок 8.3 Определение угла между пересекающимися прямыми, вращением вокруг оси параллельной горизонтальной плоскости проекций
Таким образом, траектория движения точки К1 определена прямой К1О1, точка О -центр окружности - траектории движения точки К. Чтобы найти радиус этой окружности найдем методом треугольника натуральную величину отрезка КО.Продолжим прямую К1О1 так чтобы |О1К"1|=|КО| . Точка К"1 соответствует точке К, когда прямые а и в лежат в плоскости параллельной П1 и проведенной через горизонталь - ось вращения. С учетом этого через точку К"1 и точки 11 и 21 проведем прямые, которые лежат теперь в плоскости параллельной П1, а следовательно и угол фи - натуральная величина угла между прямыми а и в.
Метод замены плоскостей проекций
Изменение взаимного положения проецируемой фигуры и плоскостей проекций методом перемены плоскостей проекций, достигается путем замены плоскостей П1 и П2 новыми плоскостями П4 (рис. 8.4). Новые плоскости выбираются перпендикулярно старым. Некоторые преобразования проекций требуют двойной замены плоскостей проекций (рис. 8.5). Последовательный переход от одной системы плоскостей проекций другой необходимо осуществлять, выполняя следующее правило: расстояние от новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до заменяемой оси.
Задача 1: Определить натуральную величину отрезка АВ прямой общего положений (рис. 8.4). Из свойства параллельного проецирования известно, что отрезок проецируется на плоскость в натуральную величину, если он параллелен этой плоскости. Выберем новую плоскость проекций П4, параллельно отрезку АВ и перпендикулярно плоскости П1. Введением новой плоскости, переходим из системы плоскостей П1П2 в систему П1П4 , причем в новой системе плоскостей проекция отрезка А4В4 будет натуральной величиной отрезка АВ.
Рисунок 8.4. Определение натуральной величины отрезка прямой методом замены плоскостей проекций
Задача 2: Определить расстояние от точки C до прямой общего положения, заданной отрезком АВ (рис. 8.5).
Рисунок 8.5. Определение натуральной величины отрезка прямой методом замены плоскостей проекций
В планиметрии плоскость является одной из основных фигур, поэтому, очень важно иметь ясное представление о ней. Эта статья создана с целью раскрытия этой темы. Сначала дано понятие плоскости, ее графическое представление и показаны обозначения плоскостей. Далее плоскость рассматривается вместе с точкой, прямой или другой плоскостью, при этом возникают варианты из взаимного расположения в пространстве. Во втором и третьем и четвертом пункте статьи как раз разобраны все варианты взаимного расположения двух плоскостей, прямой и плоскости, а также точки и плоскости, приведены основные аксиомы и графические иллюстрации. В заключении даны основные способы задания плоскости в пространстве.
Навигация по странице.
Плоскость – основные понятия, обозначения и изображение.
Простейшими и основными геометрическими фигурами в трехмерном пространстве являются точка, прямая и плоскость. Мы уже имеем представление о точке и прямой на плоскости . Если поместить плоскость, на которой изображены точки и прямые, в трехмерное пространство, то мы получим точки и прямые в пространстве. Представление о плоскости в пространстве позволяет получить, к примеру, поверхность стола или стены. Однако, стол или стена имеют конечные размеры, а плоскость простирается за их границы в бесконечность.
Точки и прямые в пространстве обозначаются также как и на плоскости – большими и маленькими латинскими буквами соответственно. Например, точки А и Q , прямые а и d . Если заданы две точки, лежащие на прямой, то прямую можно обозначить двумя буквами, соответствующими этим точкам. К примеру, прямая АВ или ВА проходит через точки А и В . Плоскости принято обозначать маленькими греческими буквами, например, плоскости , или .
При решении задач возникает необходимость изображать плоскости на чертеже. Плоскость обычно изображают в виде параллелограмма или произвольной простой замкнутой области.
Плоскость обычно рассматривается вместе с точками, прямыми или другими плоскостями, при этом возникают различные варианты их взаимного расположения. Переходим к их описанию.
Взаимное расположение плоскости и точки.
Начнем с аксиомы: в каждой плоскости имеются точки. Из нее следует первый вариант взаимного расположения плоскости и точки – точка может принадлежать плоскости. Другими словами, плоскость может проходить через точку. Для обозначения принадлежности какой-либо точки какой-либо плоскости используют символ «». Например, если плоскость проходит через точку А , то можно кратко записать .
Следует понимать, что на заданной плоскости в пространстве имеется бесконечно много точек.
Следующая аксиома показывает, сколько точек в пространстве необходимо отметить, чтобы они определяли конкретную плоскость: через три точки, не лежащие на одной прямой, проходит плоскость, причем только одна. Если известны три точки, лежащие в плоскости, то плоскость можно обозначить тремя буквами, соответствующими этим точкам. Например, если плоскость проходит через точки А , В и С , то ее можно обозначить АВС .
Сформулируем еще одну аксиому, которая дает второй вариант взаимного расположения плоскости и точки: имеются по крайней мере четыре точки, не лежащие в одной плоскости. Итак, точка пространства может не принадлежать плоскости. Действительно, в силу предыдущей аксиомы через три точки пространства проходит плоскость, а четвертая точка может как лежать на этой плоскости, так и не лежать. При краткой записи используют символ «», который равносилен фразе «не принадлежит».
К примеру, если точка А не лежит в плоскости , то используют краткую запись .
Прямая и плоскость в пространстве.
Во-первых, прямая может лежать в плоскости. В этом случае, в плоскости лежат хотя бы две точки этой прямой. Это устанавливается аксиомой: если две точки прямой лежат в плоскости, то все точки этой прямой лежат в плоскости. Для краткой записи принадлежности некоторой прямой данной плоскости пользуются символом «». Например, запись означает, что прямая а лежит в плоскости .
Во-вторых, прямая может пересекать плоскость. При этом прямая и плоскость имеют одну единственную общую точку, которую называют точкой пересечения прямой и плоскости. При краткой записи пересечение обозначаю символом «». К примеру, запись означает, что прямая а пересекает плоскость в точке М . При пересечении плоскости некоторой прямой возникает понятие угла между прямой и плоскостью .
Отдельно стоит остановиться на прямой, которая пересекает плоскость и перпендикулярна любой прямой, лежащей в этой плоскости. Такую прямую называют перпендикулярной к плоскости. Для краткой записи перпендикулярности используют симовл «». Для более глубокого изучения материала можете обратиться к статье перпендикулярность прямой и плоскости .
Особую значимость при решении задач, связанных с плоскостью, имеет так называемый нормальный вектор плоскости . Нормальным вектором плоскости является любой ненулевой вектор, лежащий на прямой, перпендикулярной этой плоскости.
В-третьих, прямая может быть параллельна плоскости, то есть, не иметь в ней общих точек. При краткой записи параллельности используют символ «». Например, если прямая а параллельна плоскости , то можно записать . Рекомендуем подробнее изучить этот случай, обратившись к статье параллельность прямой и плоскости .
Следует сказать, что прямая, лежащая в плоскости, делит эту плоскость на две полуплоскости. Прямая в этом случае называется границей полуплоскостей. Любые две точки одной полуплоскости лежат по одну сторону от прямой, а две точки разных полуплоскостей лежат по разные стороны от граничной прямой.
Взаимное расположение плоскостей.
Две плоскости в пространстве могут совпадать. В этом случае они имеют, по крайней мере, три общие точки.
Две плоскости в пространстве могут пересекаться. Пересечением двух плоскостей является прямая линия, что устанавливается аксиомой: если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
В этом случае возникает понятие угла между пересекающимися плоскостями . Отдельный интерес представляет случай, когда угол между плоскостями равен девяноста градусам. Такие плоскости называют перпендикулярными. О них мы поговорили в статье перпендикулярность плоскостей .
Наконец, две плоскости в пространстве могут быть параллельными, то есть, не иметь общих точек. Рекомендуем ознакомиться со статьей параллельность плоскостей , чтобы получить полное представление об этом варианте взаимного расположения плоскостей.
Способы задания плоскости.
Сейчас мы перечислим основные способы задания конкретной плоскости в пространстве.
Во-первых, плоскость можно задать, зафиксировав три не лежащие на одной прямой точки пространства. Этот способ основан на аксиоме: через любые три точки, не лежащие на одной прямой, проходит единственная плоскость.
Если в трехмерном пространстве зафиксирована и задана плоскость с помощью указания координат трех ее различных точек, не лежащих на одной прямой, то мы можем написать уравнение плоскости, проходящей через три заданные точки .
Два следующих способа задания плоскости являются следствием из предыдущего. Они основаны на следствиях из аксиомы о плоскости, проходящей через три точки:
- через прямую и не лежащую на ней точку проходит плоскость, притом только одна (смотрите также статью уравнение плоскости, проходящей через прямую и точку);
- через две пересекающиеся прямые проходит единственная плоскость (рекомендуем ознакомиться с материалом статьи уравнение плоскости, проходящей через две пересекающиеся прямые).
Четвертый способ задания плоскости в пространстве основан на определении параллельных прямых . Напомним, что две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Таким образом, указав две параллельные прямые в пространстве, мы определим единственную плоскость, в которой эти прямые лежат.
Если в трехмерном пространстве относительно прямоугольной системы координат задана плоскость указанным способом, то мы можем составить уравнение плоскости, проходящей через две параллельные прямые .
В курсе средней школы на уроках геометрии доказывается следующая теорема: через фиксированную точку пространства проходит единственная плоскость, перпендикулярная к данной прямой. Таким образом, мы можем задать плоскость, если укажем точку, через которую она проходит, и прямую, перпендикулярную к ней.
Если в трехмерном пространстве зафиксирована прямоугольная система координат и задана плоскость указанным способом, то можно составить уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой .
Вместо прямой, перпендикулярной к плоскости, можно указать один из нормальных векторов этой плоскости. В этом случае есть возможность написать
